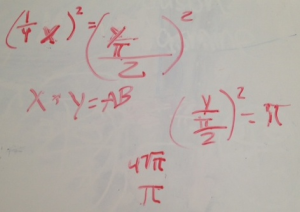My Other Math Sites
Lessons From the Classroom
What the Kids Thought
Recently Dan Meyer asks Mathalicious which of these three questions is "real world"?
Karim Ani, founder of Mathalicious, and others have opined without consensus on this particular question and on the general notion of real-world vs. fake-world problems.
I wonder what my 8th grade geometry kids think of this question.
I give them Version A on a strip of paper and ask them to work on it alone for 5 minutes. I tell them that I'm interested in learning if they understand the question as is, therefore I'm not answering any clarifying questions about it. After the 5 minutes, I put them into random groups, and they work on the problem for another 10 minutes.
Then I show them Versions B and C and ask for their preference and reason for each version.
Version A: 18 likes, 14 dislikes
Highlighted reasons for LIKING:
It gives every detail you need to know. It tells you directly all of the information. It also seems easiest to solve.
It isn't as confusing as looking at fast-motion pictures of a circle and a square. Doing math is more exact than visual guessing. [Did he translate the animation to mean guessing?]
I am able to make my own diagram and I can try to solve an equation to find out the answer.
It is simple and not confusing. It allows me to think the way I want to and not be misled by a moving picture.
With the given information, you could construct the two shapes by working backwards.
There's enough given information to make the problem interesting and hard.
I like this one the most because you can actually read the problem and refer back to it.
I think it can be solved using an equation, and be solved more easily than B and C.
It's a more accurate way to find their areas and make them equal.
I like this version because I understand the problem.
Instead of a picture of it on paper, you have to visualize it in your head first.
You can get an exact answer. It is challenging.
Version B: 18 likes, 14 dislikes
Highlighted reasons for LIKING:
It would be cool to build the animation in GSP and solve it that way.
It's a lot more simple. It provides an image and idea of what it looks like.
I can visually see when they are equal. It will be easier to see when they are equal instead of having to do a load of math.
It is visual.
I feel I have a higher chance of answering the question with a right answer.
You can easily see when the shapes have the same area.
Version C: 15 likes, 17 dislikes
Highlighted reasons for LIKING:
It seems easier because you can just count the candies and see if they're equal.
Anyone can count how many candies there are, then subtract the extra space to get the correct area.
Some students like and dislike more than one version. My takeaway on their responses:
Version A
LIKES: (see above)
DISLIKES: Not understanding the question, or "I'm a visual learner, so I like Version B better."
Version B
LIKES: It's visual. It's easy.
DISLIKES: Too fast and hard to follow. One student, "The movement is distracting and confusing. I feel like it's too abrasive and violent. Math should be more elegant than this."
Version C
LIKES: You just count the number of candies. It's visual.
DISLIKES: Too fast to follow. It seems too easy. There's space between the candies. One student, "You can't get the exact answer... And the leftover space in one shape may be more than the leftover space in the other."
I collect all their papers before telling them which version I like. I like Version A for its simplicity. I'm curious if the stated question is enough information for them to understand. This student's reason nails it for me: "It allows me to think the way I want to and not be misled by a moving picture."
We all have students who struggle with word problems. I don't think this means we should give them fewer word problems. I think it means we should give them better word problems — ones that are written with just enough information and not embedded in contrived contexts that either confuse or insult the students. And for students who need help with the question, they get to hear an explanation from a classmate.
Version B is okay, but I don't want to start with it because I feel I'd be wasting a perfectly good question in Version A! I'd reach for a piece of string to explain this question, if needed. Version C gives me a headache.
At least one person in each group understands the question, and they do their best to make sense of it in just the short 10 minutes that we have. They're trying. And making mistakes.
Our whole-class discussion at this 8th grade level:
That "arbitrary" point P is pretty darn close to the middle of A and B. You can roughly tell from using a piece of string. Or you can tell from arriving at y2/(4pi) = x2/16 (where x is distance AP forming the square's perimeter, and y is distance PB forming the circle's circumference) — the denominators are almost the same.
Likewise, P cannot be at the center because pi doesn't reconcile nicely in the equation.
We can solve for x and y using some arbitrary distance AB, and we find y to be slightly shorter.
We can ask a related question: A circle's circumference and a square's perimeter are equal, what is the area enclosed by each? Kids can certainly think about optimization and do a little bit of calculation outside of a formal calculus class.
In addition to asking the students which versions they like, I also pose Dan's exact question to them: Which of these is a "real world" math problem? Or is none of them a real-world math problem?
Their answers vary as widely as those of math educators'. However, I find this correlation that doesn't surprise me: kids who like math more do not care if the problem is real-world or not.
This [Version C] is the most "real-world" solely because of the fact that it involves a material object which in this case is the candy. However, the thing you're solving for in this question is not very "real-world" at all. Personally, I don't care at all if a problem is "real-world" or not; I just like to solve problems.
If a problem didn't have to do with "real-world" I will still do it if I like it. It doesn't really matter.
I don't think any of these problems are "real world" math problems. I like how they make me think. But I don't think I need them in the "real world."
I wouldn't care if it is a real-world problem because I was there to learn. I think all versions can be a real-world problem because it can be needed in some situations.
I feel like all of these problems are real world... But honestly it doesn't matter at all to me. It doesn't matter if it's real world or not, it doesn't affect me wanting to solve the problem.
So, one from the kids.
Venturing Into the Sequel of Penny Pyramid
I didn't get around to doing Penny Pyramid when I first saw it last year. But Dan's 3-post series and Nathan's recent mention of it were the reminders I needed to make it happen.
Act 1
how many pennies
how much money is that
how long did it take
who in their right mind would do this/who has that patience
how much does it weigh/is the table gonna collapse
what is the volume/surface area/height
what is the ratio of pennies from one level to the level above it
(Student who gave the highest high guess did correctly say her written number as "one hundred quadrillion." It made me happy that she knew this.)
Acts 2 and 3
Lauren F: Is there a way to multiply consecutive numbers quickly? You showed us the addition one...
Maddie: Isn't that the exclamation point operation?
Gabe: But we're not multiplying consecutive numbers!
Mia: Doing 40 by 40 then by 13 gives all huge numbers, so we're doing a simpler problem, then find an equation.
Lauren P: Our group is finding a pattern and making a table.
Gwen: We're doing layer by layer. There are more of us (4 instead of 3), so it's pretty quick to divide up the work.
Gabe: I already have the answer because I was too eager to do the math, but I didn't say anything to the group. (He got the answer about 2 minutes after we formed groups.)
Julia: And I got it 3 or 4 minutes after Gabe.
Angela: And I got the answer after Julia. Without her help.
Me [to Gabe, Julia, and Angela who were in same group]: Aren't you guys special. You seriously just sat there and did nothing then while I walked around?
Julia: Well, yeah, we're kinda admiring our work.
Me: Geez Louise. What do you think I'd have asked you if I knew you'd found the answer to this pyramid?
Gabe: If it was 100 high?
Me: No. A million high. A billion high.
Gabe: Hehe. That's why we didn't want to say that we're done.
Two students figured out why each stack had 13 pennies.
Their other questions were answered to their satisfaction, except we didn't know exactly how long it took Mr. Bezos to build it, but we talked about how we might be able to estimate this.
Kids remembered from last week's lesson that a square pyramid has 1/3 the volume of a cube with same dimensions, but that our penny pyramid had jagged lateral edges.
While everything up to this point had gone as well as I'd expected. Kids immediately responded to the video with WOAHs and WOWs. They asked solid questions in both Acts 1 and 2. They worked well in groups.
However, the kids and I knew that no one really struggled with the task of just finding the number of pennies. The math was pretty basic and with a calculator, 40 layers of pennies didn't make anyone break a sweat.
What was meant as an "extension" or "sequel" really needed to now become the focus of our lesson — at least for this group of students who valued a good struggle. We needed to try to figure out the equation for this penny pyramid.
But I also realized that it would be very unlikely for my 8th graders to come up with the equation because it involved summation of a sequence. (You're right, Nathan, it is unlikely, even for Gabe.) But the process of getting there might be worth it. I wouldn't be their teacher if I didn't ask them to explore the patterns that they might see along the way.
I gave them small interlocking cubes and colored chips so they could build smaller models of the pyramid.
Their collective frustration arose from how "simple" the pyramid was built — nothing more than a sum of layers whose square dimensions were consecutive.
Incomplete Cube
We started with a smaller problem. We did a 5 x 5 square pyramid with a height of 5. We didn't like the "jagged" lateral edges of the pyramid either, hence we pushed the cubes into one corner like this so at least the cubes stacked squarely.
One way would be to imagine that we had a whole 5 x 5 x 5 cube, then subtract from this the small cubes that were missing. We noticed the missing pieces were these L-shapes.
We see a pattern in these missing L-shapes:
4 pieces of (2n-1) or (n-1)(2n-1) or (2n^2)-3n+1
3 pieces of [2(n-1)-1] or (n-2)(2n-3) or (2n^2)-7n+6
2 pieces of [2(n-2)-1] or (n-3)(2n-5) or (2n^2)-11n+15
1 piece of [2(n-3)-1] or (n-4)(2n-7) or (2n^2)-15n+28
Incomplete Rectangle
How else can we see this pyramid? Because my mind has a tendency to reshape things into rectangles, I flattened the pyramid into an incomplete rectangle like this:
The dimensions of the rectangle were straightforward enough, and unlike the missing L-shapes of the incomplete cube, the missing pieces here were rectangular and came in pairs. For example, in the above right sketch, the missing pieces were two 1 x 4 and two 2 x 3 rectangles. But if n were even, then the number of missing pieces would be pairs of rectangles plus 1 lone square piece.
I talked with them about the sigma notation, and since they knew how to add {1 + 2 +... + n} quickly — we refer to this as "Gauss addition" in class — they thought it was fun to learn the new symbol.
Then we went into WolframAlpha and typed in what we wanted. The equation came up with the "newly" learned summation notation.
The kids saw patterns. They learned a fancy new sign. They knew that the right math could help solve for any penny pyramid. But I really think they look forward to learning more math in high school.
I'd like to feature this comment from the old blog:
May 19, 2013 2:21 PM
l hodge wrote:
If you draw two copies of the rectangle sketch mirroring each other, with a 1 unit space between them, you have a nice sum of squares proof. The space between the two copies is easily seen as a re-arranged sum of squares. Divide the area of expanded rectangle by 3 and you have your formula.
May 20, 2013 2:41 PMfawnnguyen wrote:
Thank you, l hodge! Mind blown. So happy to know that we were on the right track of flattening out the pyramid into an incomplete triangle. We did make another copy of the flattened pyramid but turned it around (1800 rotation) to look at that double-pyramid-with-extra-spaces rectangle, but time ran out. So, we drew this together in class today. So #nguyening!!
Stack 'em High
My algebra kiddos are doing Dan Meyer's Stacking Cups because Andrew Stadel did the lesson and wrote glowingly about it. But Andrew used only one-size cups, I used three different sizes.
Just eyeballing
I ask students to look at me, look at this 12-oz Styrofoam cup that I'm holding, and estimate how many cups they would need to stack to reach my height. I tell them I will not answer any clarifying questions regarding this, "just make your estimate in whatever way you think I mean by this." (Their hands shoot up anyway, but I remind them I won't answer any questions right now. It's clear that they want me to define "stack.")
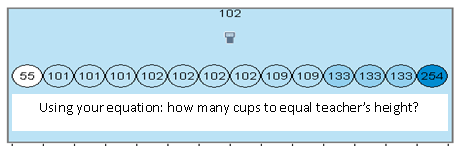
They write their answers on a quarter sheet of paper. Here are their 29 estimates, the median at 24 cups.
Given the heights
Then I tell them my height is 163 cm with the flat shoes that I have on. I carefully measure the cup's height in front of them, we get 11.25 cm.
Equipped with this knowledge, I ask the same question as above. Their 28 answers yield a median of 14 cups. Of course Dan had already anticipated this — most students just divided my height by the height of the cup.
Stack 'em like this
I now ask them what it was that they'd wanted to ask me earlier. Sure enough Eddie says, "By stacking do you mean bottom-to-bottom, then top-to-top, or... one inside another?" I give him some cups to show me. At this time at least 2/3 of the kids admit that they answered the previous questions believing that I meant to stack the cups the way Eddie just described formerly. (This is consistent with the low guesses we see in the top image.)
I ask the next question, "Okay, I need you to answer the same question again of how many cups it'll take to reach the top of my head, but you now know exactly what I mean by stack, and you also know my height and the cup's height. Here, I'll even stand on this table with 6 cups stacked at my feet so you can see. Go, give me a number.
Here are their 27 estimates, and 113 is the median.
We're just getting started
I randomly pair kids up. (Normally they are in groups of 3, but I think it's better to be in pairs for this activity.) I give each pair 6 cups. They have the last 25 minutes of class to figure out:
The equation for this problem
The number of stacked cups for my height
Some groups need help with finding the y-intercept. A few groups don't know where to begin. I ask them some questions and walk away. They plan to nominate me in June as their most non-helpful teacher. Whatever.
I like this group's drawing, even though the lip and body of cup do not add up correctly.
Using their equations
The majority of the groups figure that the lip of the cup is the slope, but many groups also think that the full height of the cup is the y-intercept. Using their equations to figure out the number of cups, they give me these numbers.
Not too shabby. My equation yields 102 stacked cups to reach top of my head, and that happens to be the mode and median.
And the actual number of cups is...
This is the moment they've been waiting for! I have 81 cups stacked already when the kids come in the next day, then they count out loud as each additional cup is added to reach my height. Our principal is paying us a visit today, and he keeps telling me how impressed he is with how engaged the kids are and how hands-on the lesson is. He helps with the countdown too and officially announces that it takes 100 cups to stack up to my height! (Three groups whose estimates of 99, 101, and 102 are having pizza with me next week!)
Getting our principal in on the fun
Working backwards. I tell the kids that it takes 116 cups to reach the top of our principal's head. How tall is he? Their answers give a median and a strong mode of 184 cm. His actual height is 183 cm!
Twice the volume and half the volume
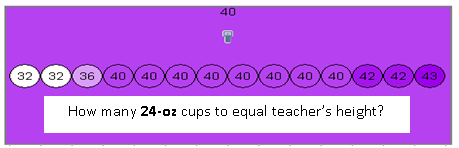
Just when they think they're done, I pull out the 24-oz and the 6-oz cups. It's not often that I hear them shriek in delight to do more math! The pair of students now gets only 3 cups of each new size. They go to work.
My height is 40 24-oz cups and 126 6-oz cups. Their calculations are great for the big cups, not so much for the little ones.
This ranks up there as one of my favorite lessons. Thanks much to Dan for another fab activity. But due to us having already passed linear equations, I honestly would not have done this lesson now without Andrew's push.
Updated 02/06/13
Eight more kids will join me for a pizza lunch for getting the equations to the 24-oz cups correctly. And here's a pic of me and the 3 stacks. The boys are 6th graders helping me hold up the stacks.
Equilateral Triangles
Thank you to Dan Meyer for this great task idea on equilateral triangles.
Act One is this video, which asks for a ranking of how well each teacher had drawn his equilateral triangle.
But as soon as I saw the video, two thoughts came up:
We’re in a 0:1 classroom right now, and having the whole class come up to the big screen just isn’t efficient.
I want to be in the competition! The kids will all want to do this.
So I knew this would have to be a pencil-to-paper activity in my class.
Eyeballing
My instructions to twenty 8th-grade geometry students:
Here’s a blank sheet of paper for you to do this task. Be sure your pencil is sharpened. Put your name in the upper-right corner.
Using only your eyeballing skill and your pencil, mark three dots in the shape of an equilateral triangle.
Gabe normally asks amazing questions that make my heart sing. Today he asked, “So you want us to draw the best equilateral triangle?” I replied, “No, Gabe, I want the crappiest one you can draw.”
Now, connect the dots with a straightedge.
Pass your papers forward. I’m going to make a photocopy of your drawing so I can have a clean copy of it just in case.
While I’m making the copies, I want you to think about how you're going to decide which triangle is most equilateral.
I dashed quickly to the copy room a few doors down. I wish you wouldn’t tell anyone that I left the children unattended for 3 minutes.
I’m now going to randomly pass the papers back, meaning you should have someone else’s drawing to work with. Write your name on their paper as the “tester.”
Okay, I want to know which one of you drew the bestest equilateral triangle. To do that, we need to come up with some kind of criteria—a way to test it, a way to score it. Talk to me.
They said that an equilateral triangle had to have three congruent sides or three 60-degree angles.
So I said:
I guess you’ll be measuring the sides and angles. Then you get these six numbers. Do you need all six? What are you going to do with the numbers?
We know what perfection looks like: 3 congruent segments, 3 congruent angles. Let us safely assume that no one drew a perfect triangle. So how far from perfect is it? What score would it get? How fair is your test?
I need you to work quietly by yourself for now. Get your tools: ruler, protractor, compass, calculator—whatever. Then figure out a way to test for equilateralness.
Working Alone
They worked diligently and carefully. I appreciated seeing one student use her ruler to extend the side length to help her spot the angle measure more accurately. Julia asked, “Measure in centimeters, right? To the tenth?”
Working in Small Groups
Now I’m going to randomly put you in groups of three. In your small group, share your scoring strategy. Fight about it. Defend your methods. Eventually, I’ll ask you to choose the best method from your group to present to the class.
By the way, just because someone in your group is in possession of a drawing that you know is far from perfect doesn’t mean their method for testing it should be dismissed.
Oh, hey—should a larger triangle deserve more points in your scoring system? I mean, is it harder to throw down three dots that are spaced farther apart?
I moved from group to group, listening to their discussions and observing their calculations.
Watching them, listening to them, asking them questions—I didn’t want to be anywhere else.
Presenting to the Whole Class
One by one, the groups were eager to share. They questioned each other:
Why 100? Why 30? Why divide by 3?
Summary of what they shared on the board. You can see that 4 of 7 groups used either side lengths or angle measures and not both.
Voting on the Best One
The scoring method from Gianna’s group got the most votes—with 9. Gabe volunteered, “None of these is spot on. But I don’t know what the best way is either.”
I said, “Thanks for saying that, Gabe. Me neither. But I love what you guys are all coming up with!”
Over two days, no one mentioned using perimeter or area. And I vowed not to say anything—I wanted the kids to drive this entire lesson to wherever it needed to go. Okay, Gianna’s famous now. We’ll refer to her group’s method as Gianna’s formula from now on.
I need everyone to go back to the triangle you have and use this formula to find a score for it.
Testing Another Triangle
I made another set of copies from the originals (during my prep this time) and randomly passed these out. This very diligent work was still human, and I just felt each triangle deserved another pair of fresh eyes on it.
Now, you’re going to apply Gianna’s formula to another triangle. This way, each person’s triangle gets tested by two different classmates.
Record your numbers on the board.
About 7 of the 20 sets of numbers had enough variance that I had to ask both scorers of each set to re-do their calculations and/or measurements. I then took the average of the two scores.
The Results
I went back to the kids’ original drawings and measured all the sides (with a ruler, thanks), applied Dan’s formula using this calculator, and here are the results.
The names highlighted in yellow share the same rankings via Dan’s and Gianna’s formulas. The greens are off by just one.
We thought this lesson was pretty great. Maia said, "Our way was not too bad at all.”
Mr. Meyer's Taco Cart
Won’t be long before I have to change the post title to Dr. Meyer’s Taco Cart. This lesson went really well today.
Act 1:
We watched the video clip. Their guesses:
Me: That was fun. Kinda split in the middle there with your guesses. But that question of who gets there first only gave you two choices—Dan or Ben. What other fun questions could we ask?
Student 1: The length of the road.
Me: I did say fun.
Student 2: What their walking rates are?
Me: That’s funner than “length of the road”?
Nathan: What is the fastest route?
Me: What do you mean by that? Can you come up and show the class what you meant?
Nathan came up and traced out the blue path with his finger:
“They can walk to the cart like this…”
Me: Oh, okay—what is the fastest route? Yeah, right, because what if neither of the guys’ routes was the fastest? This gives us a bunch of different guesses. Or a similar question: Where on the road should Dan or Ben enter to reach the taco in the shortest amount of time?
I gave each student [this working placemat] (Dan’s Act 2 slide) as their workspace, along with road strips to throw down a guess. They had to line up the road-on-paper perfectly with the road-on-strip before marking their guess so that both marks indicated the same position.
Their guesses:
Act 2:
The questions began.
Me: Okay, so now figure out how much time it takes to walk the route you chose.
Student: Can we have the dimensions?
Me: Which one?
Student: All of them.
Me: Wrong answer. Try again.
They yelled out for the legs, the sides, the road, the hypotenuse.
Me: I’m just gonna give you one of the sides. Just one. Ask wisely.
For whatever reason, they agreed it should be the hypotenuse.
(Dan didn’t give the length of the hypotenuse on his slide. I purposely put a white box there pretending like maybe they could ask for it too.)
I gave them the hypotenuse as 650.0 feet. They stared back at me, faces scrunched up like they were begging. They knew they needed another length to use their trusty little equation, a^2 + b^2 = c^2.
I also gave them the walking rates on sand and on road. I walked around the room, peeking to see what they were doing on their papers. One student plugged the rates into the equation. He wrote this:
The 2 and 5 in the bottom equation came from the walking rates. The 105625 seemed to have come from multiplying the distance (650 feet) by the time to walk that distance on sand (325 seconds), then dividing this number by 2.
Half of them were just quiet—daydreaming, thinking.
Almost 10 minutes had passed.
Me: I gave you the hypotenuse, correct? But before I gave you the hypotenuse, don’t you have the hypotenuse on your paper?
Five seconds went by, then…
Gabe: Proportions!
Lauren: Oh my God, I hate that when I think too hard!
Nathan: I thought about measuring!
Janelly: Me too! But I was afraid to.
Maia: Do you measure with a ruler?
Janelly: No. Measure with your toe.
Ha! Measure with your toe!!
How can I not love these kids?
So they got busy with their rulers.
Maia: Should we measure in inches or in centimeters?
Someone: Centimeters! We never measure in inches in here.
Me: Not never. But why might we want to measure in centimeters for this problem?
Someone else: It'll be more accurate.
They measured carefully and checked each other’s proportions. And because I only gave them the hypotenuse, their calculations for the legs weren’t all the same—but close enough. We respected the margin of error when using a ruler.
It was another day that I didn’t want this class to end. But with only five minutes left, I had to wrap up the lesson.
Me: What’s the chance that your guess happened to be the fastest route?
Various students:
Not likely.
Way off.
I think mine is perfect—I picked exactly halfway on the road.
More to the left, I think.
Me: So, after you figure out the time for your route tonight, I want you to pick another point on the road. Do two sets of calculations.
Nicole: Like do it again for a different location?
Me: Yes. And if you chose your second point to be to the left of your original guess, then why? Or to the right—why?
Thomas: Will you tell us who got closest tomorrow?
Me: Sure. I have your original guesses already [on the strips]. And guess what? The student with the closest answer gets a Del Taco lunch!
Students: Really? What about Taco Bell? I love tacos! I hope mine is closest! Are we taking a field trip there??
Me: Fine. Taco Bell or Del Taco, your choice.
Act 3:
We’ll have to wait until tomorrow to see everyone’s work and answers for their chosen paths. I’ll reveal this again with the green line drawn in to indicate the best spot to enter the road.
It would be so cool to get some numbers right near the minimum time. Maybe I’ll bring up differentiation. Maybe we’ll plug something into Wolfram Alpha.
What made this lesson work for my kids:
Nathan’s question of “what is the fastest route?” allowed for more entry points than just “who would get there first, Dan or Ben?”
Giving them just one side of the triangle was the best thing I did for this group. Once they figured out the other legs, they just tapped away on their calculators—already comfortable with the equations they’ve worked with before.
The strips gave me an easy way to display student guesses.
Printing out Dan’s Act 2 slide as work placemats gave everyone uniform access to the beach scene and made measuring the triangle sides possible.
I only thought to ask the kids to pick another point to calculate for homework seconds before I said it. Glad I did—because now we doubled our data points!
The promise of Del Taco.
Okay, no—I can’t just give lunch to the kid with the closest answer. I’ll make sure I bring in enough for the class.
This fun lesson deserves a fun closing.
Thank you, Dan.
Updated 11/07/12
Last Math Lessons
On the first day of school, I promised all my students that I'd do my best to make math relevant and challenging. I also promised to never waste their time, therefore they could expect to do math every day in my class, including the last day of class.
I did not promise them that math would be fun because doing math is always fun to me. I gave out math puzzles at my kids' birthday parties when they were younger, also at a baby shower that I gave, and of course at my own wedding.
Math 6
I called this lesson How Many Regions? (Adapted from AIMS)
I gave each student a piece of 4-by-4-inch paper and a handful of 6-inch long thin strips of construction paper. Each strip placed on the square paper would represent a "cut."
Question: What is the maximum number of regions that you can divide the square into using n number of "cuts"?
We did the first two cuts together as a class, and each student kept track of the data in their journal.
Because the goal was to get the maximum number of regions from the cuts, the kids learned quickly that the cuts needed to intersect. For example, two non-intersecting cuts created only 3 regions. A kid yelled out, "Parallel cuts!" Gotta forgive kids who blurt out academic language!
This class has been working with a pattern worksheet almost every Monday in my class, so they know to look for a recursive rule and try to find the equation for the nth term. Recursively, they saw the pattern, so it didn't take long for them to figure out that for any n (cuts), the maximum number of regions is the sum of n and the number of regions from the previous n.
With 30 seconds left of class, I told them my gift to them was to try and figure out the equation. Matt asked, "Can I email you then over the summer?"
Algebra 1
Our 8th graders' last day of classes was yesterday (Wednesday). They'll show up this evening for their promotional ceremony, dressed to the hilt.
I needed a quick one-period lesson, so I had them make 2012 Clocks. This is a common assignment: using all 4 digits in "2012" and each digit only once, they had to create expressions that would equal to the hours of 1 through 12 on a clock.
Geometry
I've seen different versions of this problem; the first time I worked on it was when it involved 3,000 bananas and 1 camel traveling 1,000 miles. I know there's a perfectly good strategy called "solve a simpler problem," but we could also start with a simpler one!
I gave my kids Desert Crossing, also from AIMS:
You live in a desert oasis and grow miniature watermelons that are worth a great deal of money, if you can get them to the market 15 kilometers away across the desert. Your harvest this year is 45 melons, but you have no way to get them to the market, except to carry them across the desert. You have a backpack that holds up to 15 melons, the maximum number that you can carry at a time. To walk across the desert, you need a certain amount of fluid and nourishment that is supplied by the melons you carry. For each kilometer you walk (in either direction), one melon must be eaten.Your challenge is to find a way to get as many melons as possible to market.
As I type this, Slater does not know that I will be awarding him the Math Excellence Award at the Promotional Ceremony this evening.
Here is Slater's work that shows one way to get the correct answer of 8 watermelons.
I did this a few weeks ago and forgot all about it; so here's a little blurb on it.Each student quickly constructed these two prisms from two same size papers.
(Dan Meyer folded them into cylinders.)
Question: Pretend the two prisms have bottoms on them, which one holds more popcorn? Take a look... Okay, grab the one you think holds more, or grab both if you think they're both equal.
And this was how they grabbed:
Then they measured and calculated the volume.
My favorite student comment: The tallness didn't make up for the fatness.
Estimating volume is a funny thing.